การยกกำลัง คือการดำเนินการทางคณิตศาสตร์อย่างหนึ่ง เขียนอยู่ในรูป an ซึ่งประกอบด้วยสองจำนวนคือ ฐาน a และ เลขชี้กำลัง (หรือ กำลัง)n การยกกำลังมีความหมายเหมือนการคูณซ้ำ ๆ กัน คือ a คูณกันเป็นจำนวน n ตัว เมื่อ n เป็นจำนวนเต็มบวก
คล้ายกับการคูณซึ่งมีความหมายเหมือนการบวกซ้ำ ๆ กัน
โดยปกติเลขชี้กำลังจะแสดงเป็นตัวยกอยู่ด้านขวาของฐาน จำนวน an อ่านว่า a ยกกำลัง n หรือเพียงแค่ a กำลัง n ในภาษาอังกฤษอาจเรียกการยกกำลังบางตัวต่างออกไปเช่น a2 จะเรียกว่า square และ a3 เรียกว่า cube เป็นต้น เมื่อตัวยกไม่สามารถใช้ได้เช่นในข้อความแอสกี ก็มีรูปแบบการเขียนอย่างอื่นที่ใช้กันอาทิ a^n และ a**n เป็นต้น
เลขยกกำลัง an อาจนิยามให้ n เป็นจำนวนเต็มลบก็ได้เมื่อค่า a ไม่เป็นศูนย์ ตามปกติไม่สามารถกระจายจำนวนจริง a กับ n ได้ทุก ๆ ค่าโดยธรรมชาติ แต่เมื่อฐาน a เป็นจำนวนจริงบวก จำนวน an สามารถนิยามเลขชี้กำลัง n ได้ทุกค่าแม้แต่จำนวนเชิงซ้อนผ่านฟังก์ชันเลขชี้กำลัง ez ฟังก์ชันตรีโกณมิติก็สามารถเขียนให้อยู่ในรูปของการยกกำลังได้
การยกกำลังที่มีเลขชี้กำลังเป็นเมทริกซ์ใช้สำหรับการหาคำตอบของระบบสมการเชิงอนุพันธ์เชิงเส้น
การยกกำลังก็ใช้งานในความรู้สาขาอื่นอย่างแพร่หลายเช่นเศรษฐศาสตร์ ชีววิทยา เคมี ฟิสิกส์ และวิทยาการคอมพิวเตอร์ ในการใช้งานคำนวณอย่างเช่นดอกเบี้ยทบต้น การเพิ่มประชากร จลนพลศาสตร์เคมี พฤติกรรมของคลื่น และการเข้ารหัสลับแบบกุญแจอสมมาตร เป็นต้น
เลขชี้กำลังเป็นจำนวนเต็ม
การดำเนินการยกกำลังด้วยเลขชี้กำลังที่เป็นจำนวนเต็ม เป็นข้อกำหนดที่จำเป็นของพีชคณิตมูลฐานเท่านั้น
เลขชี้กำลังเป็นจำนวนเต็มบวก
นิพจน์ a2 = a·a เรียกว่า square หมายถึงรูปสี่เหลี่ยมจัตุรัส (ดูเพิ่มที่การยกกำลังสอง) เพราะรูปสี่เหลี่ยมจัตุรัสที่มีด้านยาวด้านละ a หน่วย มีพื้นที่เท่ากับ a2 ตารางหน่วย
นิพจน์ a3 = a·a·a เรียกว่า cube หมายถึงทรงลูกบาศก์ (ดูเพิ่มที่การยกกำลังสาม) เพราะทรงลูกบาศก์ที่มีด้านยาวด้านละ a หน่วย มีปริมาตรเท่ากับ a3 ลูกบาศก์หน่วย
เลขชี้กำลังเป็นตัวบ่งบอกว่าจะนำฐานมาคูณกันกี่ตัว (ไม่ใช่คูณกันกี่ครั้ง) ตัวอย่างเช่น 35 = 3·3·3·3·3 = 243 ดังนี้ฐาน 3 ปรากฏ 5 ครั้งในการคูณเพราะเลขชี้กำลังเป็น 5; ค่า 243 เป็น กำลัง ของ 3 คือผลลัพธ์ที่ได้จาก 3 ยกกำลัง 5
การยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก อาจนิยามได้จากความสัมพันธ์เวียนเกิด an+1 = a·an โดยให้เงื่อนไขเริ่มต้นเป็น a1 = a
เลขชี้กำลังเป็น 0 หรือ 1
เนื่องจาก a1 หมายถึงผลคูณของ a เพียง 1 ตัว ซึ่งถูกนิยามให้มีค่าเท่ากับ a
จากความสัมพันธ์เวียนเกิดอีกรูปแบบหนึ่ง an − 1 = an/a เมื่อสมมติให้ n = 1 จะได้ a0 = 1
หรือกล่าวอีกทางหนึ่งว่า กำหนดให้ n, m, และ n−m เป็นจำนวนเต็มบวก (โดยที่ a ไม่เท่ากับศูนย์) จะได้ความสัมพันธ์
ในกรณีที่ n และ m มีค่าเท่ากัน สมการดังกล่าวจะกลายเป็น
เนื่องจากตัวเศษและตัวส่วนมีค่าเท่ากัน ดังนั้นจึงสามารถนิยามค่าของ a0 = 1 นำไปสู่กฎสองประการ
- จำนวนใด ๆ ยกกำลัง 1 จะได้ตัวมันเอง
- จำนวนใด ๆ ที่ไม่เป็นศูนย์ ยกกำลัง 0 จะได้ 1 ซึ่งเป็นการตีความมาจากผลคูณว่าง สำหรับกรณี 00 ดูเพิ่มที่หัวข้อ 0 ยกกำลัง 0
ความหมายทางคณิตศาสตร์เชิงการจัด
สำหรับ n และ m ที่เป็นจำนวนเต็มไม่เป็นลบ (จำนวนเต็มบวกรวมทั้งศูนย์) เลขยกกำลัง nm จะหมายถึงภาวะเชิงการนับ (cardinality) ของเซตของm สิ่งอันดับ (m-tuple) ที่ได้จากเซตที่มีสมาชิก n ตัว หรือพูดอีกนัยหนึ่งคือ เป็นจำนวนของคำที่มีตัวอักษร m ตัว จากชุดตัวอักษร n ตัว
| 05 = │ {} │ = 0 | ไม่มีห้าสิ่งอันดับ จากเซตว่าง |
| 14 = │ { (1, 1, 1, 1) } │ = 1 | มีสี่สิ่งอันดับ 1 ชุด จากเซตที่มีสมาชิก 1 ตัว |
| 23 = │ { (1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2) } │ = 8 | มีสามสิ่งอันดับ 8 ชุด จากเซตที่มีสมาชิก 2 ตัว |
| 32 = │ { (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) } │ = 9 | มีสองสิ่งอันดับ (คู่อันดับ) 9 ชุด จากเซตที่มีสมาชิก 3 ตัว |
| 41 = │ { (1), (2), (3), (4) } │ = 4 | มีหนึ่งสิ่งอันดับ 4 ชุด จากเซตที่มีสมาชิก 4 ตัว |
| 50 = │ { () } │ = 1 | มีศูนย์สิ่งอันดับ 1 ชุด จากเซตที่มีสมาชิก 5 ตัว |
ดูเพิ่มเติมที่หัวข้อการยกกำลังบนเซต
เลขชี้กำลังเป็นจำนวนเต็มลบ
จากนิยาม จำนวนใด ๆ ที่ไม่เป็นศูนย์ เมื่อยกกำลังด้วย −1 จะทำให้เกิดส่วนกลับหรือตัวผกผันการคูณ
จึงสามารถนิยามว่า
เมื่อ a เป็นจำนวนใด ๆ ที่ไม่เป็นศูนย์และ n เป็นจำนวนเต็มบวก แต่สำหรับจำนวน 0 ยกกำลังจำนวนลบ จะทำให้เกิดกรณีการหารด้วยศูนย์ จึงไม่มีการนิยาม
นิยามของ a−n สำหรับค่า a ใด ๆ ที่ไม่ใช่ศูนย์ ทำให้เอกลักษณ์ aman = am+n เป็นจริงบนทุกช่วงจำนวนเต็มของ m กับ n (ทั้งบวก ลบ และศูนย์) จากเดิมเป็นจริงเฉพาะเมื่อ m กับ n เป็นจำนวนเต็มไม่เป็นลบ โดยเฉพาะอย่างยิ่งการใช้เอกลักษณ์นี้โดยกำหนดให้ m = −n จะทำให้
เมื่อ a0 ได้นิยามเช่นนั้นแล้ว เป็นเหตุให้นำไปสู่การนิยาม a−n = 1/an ดังที่ได้กล่าวแล้ว
การยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มลบ อาจสามารถเขียนให้อยู่ในรูปของการหารซ้ำ ๆ จาก 1 ด้วยฐานก็ได้ ตัวอย่างเช่น
-
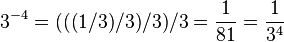
เอกลักษณ์และสมบัติ
เอกลักษณ์สำคัญที่สุดของการยกกำลังที่สอดคล้องกับกรณีเลขชี้กำลังเป็นจำนวนเต็มคือเอกลักษณ์นี้จึงเป็นผลที่ตามมาและเอกลักษณ์พื้นฐานอีกอันหนึ่งคือในขณะที่การบวกและการคูณมีสมบัติการสลับที่ เช่น 2+3 = 5 = 3+2 และ 2·3 = 6 = 3·2 แต่การยกกำลังไม่มีสมบัติการสลับที่ เช่น 23 = 8 แต่32 = 9และเช่นเดียวกัน ในขณะที่การบวกและการคูณมีสมบัติการเปลี่ยนหมู่ เช่น (2+3) +4 = 9 = 2+ (3+4) และ (2·3) ·4 = 24 = 2· (3·4) แต่การยกกำลังไม่มีสมบัติการเปลี่ยนหมู่ ตัวอย่างเช่น "23 ยกกำลัง 4" จะได้ผลลัพธ์เป็น 84 หรือเท่ากับ 4,096 แต่ "2 ยกกำลัง 34" จะได้ผลลัพธ์เป็น 281 หรือ2,417,851,639,229,258,349,412,352 ถ้าหากเขียนเลขยกกำลังซ้อนกันโดยไม่ใส่วงเล็บ ลำดับของการคำนวณจะทำจากตัวบนสุดมาก่อน นั่นคือ-

กำลังของ 10
ในระบบเลขฐานสิบ กำลังจำนวนเต็มของ 10 สามารถเขียนแทนได้ด้วยเลข 1 ตามด้วยหรือนำโดยเลข 0 จำนวนหนึ่ง ซึ่งพิจารณาจากเครื่องหมายและขนาดของเลขชี้กำลัง ตัวอย่างเช่น 103 = 1,000 และ 10−4 = 0.0001 เป็นต้นการยกกำลังด้วยฐาน 10 ถูกใช้ในสัญกรณ์วิทยาศาสตร์ เพื่อใช้อธิบายจำนวนขนาดใหญ่หรือเล็กมาก ตัวอย่างเช่น จำนวน 299,792,458 เมตรต่อวินาที (ความเร็วแสงในสุญญากาศ) สามารถเขียนได้เป็น 2.99792458×108 m/s หรือเท่ากับประมาณ 2.998×108 m/sคำอุปสรรคในหน่วยเอสไอที่มีพื้นฐานบนกำลังของ 10 ก็ถูกใช้อธิบายปริมาณที่ใหญ่หรือเล็กมากได้เช่นกันเช่น คำอุปสรรค กิโล หมายถึง 103 = 1,000 ดังนั้น 1 กิโลเมตรจึงเท่ากับ 1,000 เมตรกำลังของ 2
กำลังจำนวนเต็มบวกของ 2 เป็นสิ่งที่สำคัญในวิทยาการคอมพิวเตอร์ เพราะว่าตัวแปรฐานสองขนาด n บิต จะมีค่าที่เป็นไปได้ทั้งหมด 2n ค่ากำลังของ 2 ก็เป็นสิ่งสำคัญในทฤษฎีเซต เนื่องจากเซตเซตหนึ่งที่มีสมาชิก n ตัว จะมีเซตกำลังที่มีสมาชิก 2n ตัว (เซตกำลังคือเซตของเซตย่อยทั้งหมดจากเซตต้นแบบ)กำลังจำนวนเต็มลบของ 2 ก็ใช้กันทั่วไป เช่น 2−1 = 12 หมายถึงครึ่ง (half), 2−2 = 14 คือหนึ่งในสี่ (quarter) เป็นต้นในระบบเลขฐานสอง กำลังจำนวนเต็มของ 2 ก็สามารถเขียนแทนได้ด้วยเลข 1 แล้วตามด้วยหรือนำโดยเลข 0 ซึ่งพิจารณาจากเครื่องหมายและขนาดของเลขชี้กำลัง ตัวอย่าง 23 เขียนในเลขฐานสองว่า 10002 เป็นต้นกำลังของ 1
กำลังจำนวนเต็มของ 1 ทุกจำนวนมีค่าเท่ากับ 1 นั่นคือ 1n = 1กำลังของ 0
ถ้าเลขชี้กำลังเป็นจำนวนบวก เลขยกกำลังของ 0 จะได้ 0 นั่นคือ 0n = 0; n > 0ถ้าเลขชี้กำลังเป็นจำนวนลบ เลขยกกำลังของ 0 จะไม่นิยาม เนื่องจากทำให้เกิดการหารด้วยศูนย์ถ้าเลขชี้กำลังเป็นศูนย์ ผู้แต่งตำราบางท่านได้นิยามว่า 00 = 1 ในขณะที่บางท่านก็คงไว้ว่าไม่นิยาม ดูที่หัวข้อ 0 ยกกำลัง 0กำลังของ −1
ถ้า n เป็นจำนวนคู่ จะได้ (−1) n = 1ถ้า n เป็นจำนวนคี่ จะได้ (−1) n = −1จากสมบัติดังกล่าว กำลังของ −1 จึงมีประโยชน์ในการแสดงลำดับที่มีการสลับเครื่องหมาย ส่วนกรณีที่คล้ายกันสำหรับจำนวนเชิงซ้อน i ดูที่หัวข้อกำลังของจำนวนเชิงซ้อนเลขชี้กำลังขนาดใหญ่
ลิมิตของลำดับของกำลังของจำนวนที่มากกว่า 1 จะลู่ออก หมายความว่าจะมีค่าเพิ่มขึ้นเรื่อย ๆ โดยไม่จำกัด-
- an → ∞ เมื่อ n → ∞ ถ้า a > 1
อาจเรียกได้ว่า a ยกกำลัง n จะมีค่าเข้าใกล้อนันต์ถ้า n มีค่าเข้าใกล้อนันต์ เมื่อ a มีค่ามากกว่า 1สำหรับกำลังของจำนวนที่มีค่าสัมบูรณ์น้อยกว่า 1 ลิมิตของลำดับจะลู่เข้าค่า 0-
- an → 0 เมื่อ n → ∞ ถ้า |a| < 1
และกำลังของ 1 จะได้ค่า 1 เสมอ-
- an = 1 สำหรับทุกค่าของ n ถ้า a = 1
แต่หากฐาน a มีค่าเข้าใกล้ 1 พร้อมกับเลขชี้กำลังมีค่าเข้าใกล้อนันต์ ลิมิตของมันไม่สำคัญว่าจะต้องเท่ากับ 1 ตัวอย่างกรณีหนึ่งที่สำคัญคือ-
- (1 + n−1) n → e เมื่อ n → ∞
กำลังจำนวนจริงของจำนวนจริงบวก
การยกกำลังจำนวนจริงบวก ด้วยเลขชี้กำลังที่ไม่เป็นจำนวนเต็ม สามารถคำนวณได้สองวิธีนั่นคือ- เลขชี้กำลังเป็นจำนวนตรรกยะ สามารถนิยามให้เป็นรากที่ n และเลขชี้กำลังที่ไม่เป็นศูนย์สามารถนิยามได้จากความต่อเนื่อง
- เลขชี้กำลังเป็นจำนวนจริง สามารถนิยามให้เป็นลอการิทึมธรรมชาติโดยใช้ฟังก์ชันเลขชี้กำลัง
เอกลักษณ์และสมบัติที่แสดงไว้ด้านบนซึ่งนิยามไว้สำหรับเลขชี้กำลังจำนวนเต็ม ก็ยังคงเป็นจริงอยู่สำหรับเลขชี้กำลังจำนวนจริงบวกที่ไม่ใช่จำนวนเต็ม อย่างไรก็ตามเอกลักษณ์นี้ไม่สามารถขยายแนวคิดได้อย่างคงเส้นคงวาถ้า a เป็นจำนวนจริงลบ ดูเพิ่มที่หัวข้อรากที่ n ที่เป็นลบ ความผิดพลาดของเอกลักษณ์นี้เป็นมูลฐานของปัญหาที่เกี่ยวกับกำลังของจำนวนเชิงซ้อน ซึ่งได้อธิบายไว้แล้วที่หัวข้อความผิดพลาดของเอกลักษณ์กำลังและลอการิทึม
-
-



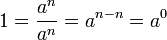


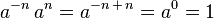


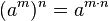
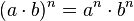

 ซึ่งทำให้สมการ
ซึ่งทำให้สมการ 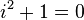 เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่นๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน
เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่นๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน  ทุกตัวสามารถเขียนอยู่ในรูป
ทุกตัวสามารถเขียนอยู่ในรูป  โดยที่
โดยที่  และ
และ  เป็นจำนวนจริง โดยเราเรียก
เป็นจำนวนจริง โดยเราเรียก  จากนิยามข้างต้นเราได้ว่าเซตของจำนวนจริงเป็นสับเซตของเซตของจำนวนเชิงซ้อน ดังนั้นจำนวนจริงทุกตัวเป็นจำนวนเชิงซ้อน เราสามารถบวก ลบ คูณ และหารสมาชิกสองตัวใดๆ ของเซตของจำนวนเชิงซ้อนได้ (เว้นแต่ในกรณีที่ตัวหารคือศูนย์) และผลลัพธ์ที่ได้จะเป็นจำนวนเชิงซ้อนเสมอ ดังนั้นในทางคณิตศาสตร์เราจึงกล่าวว่าเซตของจำนวนเชิงซ้อนเป็น
จากนิยามข้างต้นเราได้ว่าเซตของจำนวนจริงเป็นสับเซตของเซตของจำนวนเชิงซ้อน ดังนั้นจำนวนจริงทุกตัวเป็นจำนวนเชิงซ้อน เราสามารถบวก ลบ คูณ และหารสมาชิกสองตัวใดๆ ของเซตของจำนวนเชิงซ้อนได้ (เว้นแต่ในกรณีที่ตัวหารคือศูนย์) และผลลัพธ์ที่ได้จะเป็นจำนวนเชิงซ้อนเสมอ ดังนั้นในทางคณิตศาสตร์เราจึงกล่าวว่าเซตของจำนวนเชิงซ้อนเป็น ทั้งหมดโดยที่
ทั้งหมดโดยที่  และ
และ  เป็นจำนวนจริง และ
เป็นจำนวนจริง และ (การบวก) และ
(การบวก) และ  (การคูณ) โดยปฏิบัติการทั้งมีนิยามดังต่อไปนี้
(การคูณ) โดยปฏิบัติการทั้งมีนิยามดังต่อไปนี้ เป็นจำนวนเชิงซ้อนใดๆ
เป็นจำนวนเชิงซ้อนใดๆ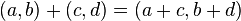
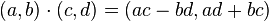
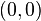

 (เขียนแทนด้วย
(เขียนแทนด้วย  ) คือ (-a,-b)
) คือ (-a,-b)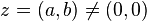 อินเวอร์สการคูณของ
อินเวอร์สการคูณของ  ) คือ
) คือ 
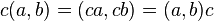 เมื่อ
เมื่อ  เป็นจำนวนจริงและ
เป็นจำนวนจริงและ  กล่าวคือเราสามารถเขียนจำนวนเชิงซ้อนทุกตัวในรูปของ
กล่าวคือเราสามารถเขียนจำนวนเชิงซ้อนทุกตัวในรูปของ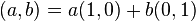
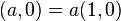 ว่าเป็นจำนวนจริง
ว่าเป็นจำนวนจริง 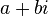 ซึ่งเป็นที่นิยมใช้มากกว่าแบบคู่ลำดับ
ซึ่งเป็นที่นิยมใช้มากกว่าแบบคู่ลำดับ นั่นคือ
นั่นคือ 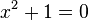 ซึ่งไม่สามารถหาคำตอบได้ในเซตของจำนวนจริง ดังนั้น เซตของจำนวนเชิงซ้อนจึงเป็น
ซึ่งไม่สามารถหาคำตอบได้ในเซตของจำนวนจริง ดังนั้น เซตของจำนวนเชิงซ้อนจึงเป็น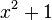 อีกนัยหนึ่ง เซตของจำนวนเชิงซ้อนคือ
อีกนัยหนึ่ง เซตของจำนวนเชิงซ้อนคือ![\mathbb{R}[x]](http://upload.wikimedia.org/math/d/3/0/d30c4d8a82d45c0e3a53461a45ca72b5.png) กับ
กับ เขียนเป็นประโยคสัญลักษณ์ได้ว่า
เขียนเป็นประโยคสัญลักษณ์ได้ว่า![\mathbb{C} = \mathbb{R}[x]/(x^2+1)](http://upload.wikimedia.org/math/5/a/c/5ac3abb6998c787c5115e49600c4e3b8.png)
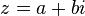 เราเรียก
เราเรียก  และเราเรียก
และเราเรียก  เราเรียกจำนวนเชิงซ้อนที่มีส่วนจริงเป็น 0 และส่วนจินตภาพไม่เป็น 0 ว่า
เราเรียกจำนวนเชิงซ้อนที่มีส่วนจริงเป็น 0 และส่วนจินตภาพไม่เป็น 0 ว่า เราเขียนแทนสังยุคของ
เราเขียนแทนสังยุคของ 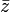 สังยุคของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้
สังยุคของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้



 ,
, 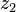 เป็นจำนวนเชิงซ้อนใดๆ
เป็นจำนวนเชิงซ้อนใดๆ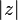 คือจำนวนจริงบวก
คือจำนวนจริงบวก  เราอาจแปลความหมายของขนาดของจำนวนเชิงซ้อนได้ว่าเป็นความยาวของเส้นตรงที่ลากจากจุด (0,0) ไปยังจุด (a,b) บน
เราอาจแปลความหมายของขนาดของจำนวนเชิงซ้อนได้ว่าเป็นความยาวของเส้นตรงที่ลากจากจุด (0,0) ไปยังจุด (a,b) บน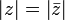


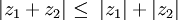 (
(
 ก็ต่อเมื่อ
ก็ต่อเมื่อ 
 ทำให้เราได้ว่าถ้า
ทำให้เราได้ว่าถ้า 

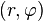 เมื่อ
เมื่อ  และ
และ  เป็นมุมที่เวกเตอร์
เป็นมุมที่เวกเตอร์  สังเกตว่าจำนวนเชิงซ้อนที่มีอาร์กิวเมนต์ต่างกันเท่ากับผลคูณของจำนวนเต็มกับ
สังเกตว่าจำนวนเชิงซ้อนที่มีอาร์กิวเมนต์ต่างกันเท่ากับผลคูณของจำนวนเต็มกับ  จะมีค่าเท่ากัน
จะมีค่าเท่ากัน


 ด้วยเหตุนี้เราจึงสามารถมองการคูณจำนวนเชิงซ้อนตัวหนึ่งๆ ว่าเป็นการหมุนและการยืด (หรือหด) เวกเตอร์ด้วยอาร์กิวเมนต์และขนาดของจำนวนเชิงซ้อนตัวนั้นตามลำดับ
ด้วยเหตุนี้เราจึงสามารถมองการคูณจำนวนเชิงซ้อนตัวหนึ่งๆ ว่าเป็นการหมุนและการยืด (หรือหด) เวกเตอร์ด้วยอาร์กิวเมนต์และขนาดของจำนวนเชิงซ้อนตัวนั้นตามลำดับ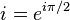 จึงสมมูลกับการหมุนเวกเตอร์ 90 องศาทวนเข็มนาฬิกา สมการ ฉะนั้นเราสามารถเข้าใจความหมายของสมการ
จึงสมมูลกับการหมุนเวกเตอร์ 90 องศาทวนเข็มนาฬิกา สมการ ฉะนั้นเราสามารถเข้าใจความหมายของสมการ  ได้อีกนัยหนึ่งว่า "การหมุน 90 องศาสองครั้งมีค่าเท่ากับการหมุน 180 องศา" หรือ "เมื่อหมุนเวกเตอร์
ได้อีกนัยหนึ่งว่า "การหมุน 90 องศาสองครั้งมีค่าเท่ากับการหมุน 180 องศา" หรือ "เมื่อหมุนเวกเตอร์  เราได้ว่า
เราได้ว่า
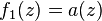 เป็นการหมุนและการยืดเวกเตอร์ ส่วนฟังก์ชัน
เป็นการหมุนและการยืดเวกเตอร์ ส่วนฟังก์ชัน 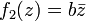 นั้นประกอบด้วยการหมุน การพลิก และการยืดเวกเตอร์ในฟังก์ชันเดียว สังเกตว่า
นั้นประกอบด้วยการหมุน การพลิก และการยืดเวกเตอร์ในฟังก์ชันเดียว สังเกตว่า 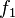 เท่านั้นที่เป็นการแปลงเชิงเส้นบน
เท่านั้นที่เป็นการแปลงเชิงเส้นบน 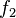 ได้ในเซตของจำนวนจริง แต่อนุพันธ์นั้นไม่สอดคล้องกับ
ได้ในเซตของจำนวนจริง แต่อนุพันธ์นั้นไม่สอดคล้องกับ ) จะมีลักษณะจำเพาะสามประการ ดังนี้
) จะมีลักษณะจำเพาะสามประการ ดังนี้