จำนวนเชิงซ้อน (อังกฤษ : complex number) ในทางคณิตศาสตร์ คือ เซตที่ต่อเติมจากเซตของจำนวนจริงโดยเพิ่มจำนวน  ซึ่งทำให้สมการ
ซึ่งทำให้สมการ 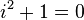 เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่นๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน
เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่นๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน  ทุกตัวสามารถเขียนอยู่ในรูป
ทุกตัวสามารถเขียนอยู่ในรูป  โดยที่
โดยที่  และ
และ  เป็นจำนวนจริง โดยเราเรียก
เป็นจำนวนจริง โดยเราเรียก  และ
และ  ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ
ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ  ตามลำดับ
ตามลำดับ
 ซึ่งทำให้สมการ
ซึ่งทำให้สมการ 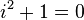 เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่นๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน
เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่นๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน  ทุกตัวสามารถเขียนอยู่ในรูป
ทุกตัวสามารถเขียนอยู่ในรูป  โดยที่
โดยที่  และ
และ  เป็นจำนวนจริง โดยเราเรียก
เป็นจำนวนจริง โดยเราเรียก  และ
และ  ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ
ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ  ตามลำดับ
ตามลำดับ
เซตของจำนวนเชิงซ้อนทุกตัวมักถูกแทนด้วยสัญลักษณ์  จากนิยามข้างต้นเราได้ว่าเซตของจำนวนจริงเป็นสับเซตของเซตของจำนวนเชิงซ้อน ดังนั้นจำนวนจริงทุกตัวเป็นจำนวนเชิงซ้อน เราสามารถบวก ลบ คูณ และหารสมาชิกสองตัวใดๆ ของเซตของจำนวนเชิงซ้อนได้ (เว้นแต่ในกรณีที่ตัวหารคือศูนย์) และผลลัพธ์ที่ได้จะเป็นจำนวนเชิงซ้อนเสมอ ดังนั้นในทางคณิตศาสตร์เราจึงกล่าวว่าเซตของจำนวนเชิงซ้อนเป็นฟีลด์ นอกจากนี้เซตของจำนวนเชิงซ้อนยังมีสมบัติการปิดทางพีชคณิต (algebraically closed) กล่าวคือ พหุนามที่มีสัมประสิทธิ์เป็นจำนวนเชิงซ้อนจะมีราก (พหุนาม)เป็นจำนวนเชิงซ้อนด้วย สมบัตินี้เป็นที่รู้จักในชื่อทฤษฎีบทมูลฐานของพีชคณิต
จากนิยามข้างต้นเราได้ว่าเซตของจำนวนจริงเป็นสับเซตของเซตของจำนวนเชิงซ้อน ดังนั้นจำนวนจริงทุกตัวเป็นจำนวนเชิงซ้อน เราสามารถบวก ลบ คูณ และหารสมาชิกสองตัวใดๆ ของเซตของจำนวนเชิงซ้อนได้ (เว้นแต่ในกรณีที่ตัวหารคือศูนย์) และผลลัพธ์ที่ได้จะเป็นจำนวนเชิงซ้อนเสมอ ดังนั้นในทางคณิตศาสตร์เราจึงกล่าวว่าเซตของจำนวนเชิงซ้อนเป็นฟีลด์ นอกจากนี้เซตของจำนวนเชิงซ้อนยังมีสมบัติการปิดทางพีชคณิต (algebraically closed) กล่าวคือ พหุนามที่มีสัมประสิทธิ์เป็นจำนวนเชิงซ้อนจะมีราก (พหุนาม)เป็นจำนวนเชิงซ้อนด้วย สมบัตินี้เป็นที่รู้จักในชื่อทฤษฎีบทมูลฐานของพีชคณิต
 จากนิยามข้างต้นเราได้ว่าเซตของจำนวนจริงเป็นสับเซตของเซตของจำนวนเชิงซ้อน ดังนั้นจำนวนจริงทุกตัวเป็นจำนวนเชิงซ้อน เราสามารถบวก ลบ คูณ และหารสมาชิกสองตัวใดๆ ของเซตของจำนวนเชิงซ้อนได้ (เว้นแต่ในกรณีที่ตัวหารคือศูนย์) และผลลัพธ์ที่ได้จะเป็นจำนวนเชิงซ้อนเสมอ ดังนั้นในทางคณิตศาสตร์เราจึงกล่าวว่าเซตของจำนวนเชิงซ้อนเป็นฟีลด์ นอกจากนี้เซตของจำนวนเชิงซ้อนยังมีสมบัติการปิดทางพีชคณิต (algebraically closed) กล่าวคือ พหุนามที่มีสัมประสิทธิ์เป็นจำนวนเชิงซ้อนจะมีราก (พหุนาม)เป็นจำนวนเชิงซ้อนด้วย สมบัตินี้เป็นที่รู้จักในชื่อทฤษฎีบทมูลฐานของพีชคณิต
จากนิยามข้างต้นเราได้ว่าเซตของจำนวนจริงเป็นสับเซตของเซตของจำนวนเชิงซ้อน ดังนั้นจำนวนจริงทุกตัวเป็นจำนวนเชิงซ้อน เราสามารถบวก ลบ คูณ และหารสมาชิกสองตัวใดๆ ของเซตของจำนวนเชิงซ้อนได้ (เว้นแต่ในกรณีที่ตัวหารคือศูนย์) และผลลัพธ์ที่ได้จะเป็นจำนวนเชิงซ้อนเสมอ ดังนั้นในทางคณิตศาสตร์เราจึงกล่าวว่าเซตของจำนวนเชิงซ้อนเป็นฟีลด์ นอกจากนี้เซตของจำนวนเชิงซ้อนยังมีสมบัติการปิดทางพีชคณิต (algebraically closed) กล่าวคือ พหุนามที่มีสัมประสิทธิ์เป็นจำนวนเชิงซ้อนจะมีราก (พหุนาม)เป็นจำนวนเชิงซ้อนด้วย สมบัตินี้เป็นที่รู้จักในชื่อทฤษฎีบทมูลฐานของพีชคณิต
นอกจากนี้ ในทางคณิตศาสตร์แล้วคำว่า "เชิงซ้อน" ถูกใช้เป็นคำคุณศัพท์ที่มีความหมายว่าฟีลด์ของตัวเลขที่เราสนใจคือฟีลด์ของจำนวนเชิงซ้อน ยกตัวอย่างเช่น การวิเคราะห์เชิงซ้อน, พหุนามเชิงซ้อน, แมทริกซ์เชิงซ้อน, และพีชคณิตลีเชิงซ้อน เป็นต้น
ฟีลด์ของจำนวนเชิงซ้อน
ฟีลด์ของจำนวนเชิงซ้อน  ประกอบด้วยเซตของคู่ลำดับ
ประกอบด้วยเซตของคู่ลำดับ  ทั้งหมดโดยที่
ทั้งหมดโดยที่  และ
และ  เป็นจำนวนจริง และปฏิบัติการสองตัวคือ
เป็นจำนวนจริง และปฏิบัติการสองตัวคือ  (การบวก) และ
(การบวก) และ  (การคูณ) โดยปฏิบัติการทั้งมีนิยามดังต่อไปนี้
(การคูณ) โดยปฏิบัติการทั้งมีนิยามดังต่อไปนี้
 ประกอบด้วยเซตของคู่ลำดับ
ประกอบด้วยเซตของคู่ลำดับ  ทั้งหมดโดยที่
ทั้งหมดโดยที่  และ
และ  เป็นจำนวนจริง และปฏิบัติการสองตัวคือ
เป็นจำนวนจริง และปฏิบัติการสองตัวคือ  (การบวก) และ
(การบวก) และ  (การคูณ) โดยปฏิบัติการทั้งมีนิยามดังต่อไปนี้
(การคูณ) โดยปฏิบัติการทั้งมีนิยามดังต่อไปนี้
ให้  และ
และ  เป็นจำนวนเชิงซ้อนใดๆ
เป็นจำนวนเชิงซ้อนใดๆ
 และ
และ  เป็นจำนวนเชิงซ้อนใดๆ
เป็นจำนวนเชิงซ้อนใดๆ
เมื่อการบวก การลบ และการคูณภายในคู่ลำดับคือการบวก การลบ และการคูณจำนวนจริง
เซตของจำนวนเชิงซ้อนและปฏิบัติการทั้งสองมีสมบัติเป็นฟีลด์ กล่าวคือ
- การบวกและการคูณมีสมบัติการปิด การสลับที่ การเปลี่ยนกลุ่ม และการแจกแจง
- มีเอกลักษณ์การบวกคือ
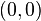
- มีเอกลักษณ์การคูณคือ

- อินเวอร์สการบวกของ
 (เขียนแทนด้วย
(เขียนแทนด้วย  ) คือ (-a,-b)
) คือ (-a,-b) - ถ้าหาก
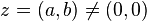 อินเวอร์สการคูณของ
อินเวอร์สการคูณของ  (เขียนแทนด้วย
(เขียนแทนด้วย  ) คือ
) คือ 
จำนวนเชิงซ้อนในฐานะปริภูมิเวกเตอร์และฟีลด์ต่อเติม
อนึ่ง เราอาจมองเซตของจำนวนเชิงซ้อนเป็นปริภูมิเวกเตอร์สองมิติบนเซตของจำนวนจริง เราสามารถใช้การบวกจำนวนเชิงซ้อนแทนการบวกเวกเตอร์ และการคูณด้วยสเกลาร์สามารถนิยามได้ดังต่อไปนี้
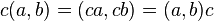 เมื่อ
เมื่อ  เป็นจำนวนจริงและ
เป็นจำนวนจริงและ  เป็นจำนวนเชิงซ้อนใดๆ
เป็นจำนวนเชิงซ้อนใดๆ
ด้วยเหตุนี้เราได้ว่าฐานหลักหนึ่งของเซตของจำนวนเชิงซ้อนประกอบด้วยเวกเตอร์  และ
และ  กล่าวคือเราสามารถเขียนจำนวนเชิงซ้อนทุกตัวในรูปของผลรวมเชิงเส้นของเวกเตอร์ทั้งสอง:
กล่าวคือเราสามารถเขียนจำนวนเชิงซ้อนทุกตัวในรูปของผลรวมเชิงเส้นของเวกเตอร์ทั้งสอง:
 และ
และ  กล่าวคือเราสามารถเขียนจำนวนเชิงซ้อนทุกตัวในรูปของผลรวมเชิงเส้นของเวกเตอร์ทั้งสอง:
กล่าวคือเราสามารถเขียนจำนวนเชิงซ้อนทุกตัวในรูปของผลรวมเชิงเส้นของเวกเตอร์ทั้งสอง:
ตามความนิยม เรามักแปลความหมายของ 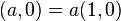 ว่าเป็นจำนวนจริง
ว่าเป็นจำนวนจริง  (ด้วยเหตุนี้เราจึงกล่าวว่าเซตจำนวนจริงเป็นสับเซตของเซตจำนวนเชิงซ้อน) และมักใช้สัญลักษณ์
(ด้วยเหตุนี้เราจึงกล่าวว่าเซตจำนวนจริงเป็นสับเซตของเซตจำนวนเชิงซ้อน) และมักใช้สัญลักษณ์  แทน
แทน  จำนวนเชิงซ้อน
จำนวนเชิงซ้อน  จึงเขียนได้อีกแบบหนึ่งว่า
จึงเขียนได้อีกแบบหนึ่งว่า 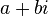 ซึ่งเป็นที่นิยมใช้มากกว่าแบบคู่ลำดับ
ซึ่งเป็นที่นิยมใช้มากกว่าแบบคู่ลำดับ
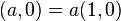 ว่าเป็นจำนวนจริง
ว่าเป็นจำนวนจริง  (ด้วยเหตุนี้เราจึงกล่าวว่าเซตจำนวนจริงเป็นสับเซตของเซตจำนวนเชิงซ้อน) และมักใช้สัญลักษณ์
(ด้วยเหตุนี้เราจึงกล่าวว่าเซตจำนวนจริงเป็นสับเซตของเซตจำนวนเชิงซ้อน) และมักใช้สัญลักษณ์  แทน
แทน  จำนวนเชิงซ้อน
จำนวนเชิงซ้อน  จึงเขียนได้อีกแบบหนึ่งว่า
จึงเขียนได้อีกแบบหนึ่งว่า 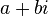 ซึ่งเป็นที่นิยมใช้มากกว่าแบบคู่ลำดับ
ซึ่งเป็นที่นิยมใช้มากกว่าแบบคู่ลำดับ
จากนิยามการคูณจำนวนเชิงซ้อนข้างต้น เราได้ว่า  นั่นคือ
นั่นคือ  เป็นคำตอบของสมการ
เป็นคำตอบของสมการ 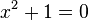 ซึ่งไม่สามารถหาคำตอบได้ในเซตของจำนวนจริง ดังนั้น เซตของจำนวนเชิงซ้อนจึงเป็นฟีลด์ต่อเติม (field extension) ของเซตของจำนวนจริงโดยการเพิ่มรากของพหุนาม
ซึ่งไม่สามารถหาคำตอบได้ในเซตของจำนวนจริง ดังนั้น เซตของจำนวนเชิงซ้อนจึงเป็นฟีลด์ต่อเติม (field extension) ของเซตของจำนวนจริงโดยการเพิ่มรากของพหุนาม 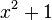 อีกนัยหนึ่ง เซตของจำนวนเชิงซ้อนคือริงผลหาร (quotient ring) ของริงพหุนาม
อีกนัยหนึ่ง เซตของจำนวนเชิงซ้อนคือริงผลหาร (quotient ring) ของริงพหุนาม ![\mathbb{R}[x]](http://upload.wikimedia.org/math/d/3/0/d30c4d8a82d45c0e3a53461a45ca72b5.png) กับไอดีล
กับไอดีล  เขียนเป็นประโยคสัญลักษณ์ได้ว่า
เขียนเป็นประโยคสัญลักษณ์ได้ว่า
 นั่นคือ
นั่นคือ  เป็นคำตอบของสมการ
เป็นคำตอบของสมการ 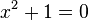 ซึ่งไม่สามารถหาคำตอบได้ในเซตของจำนวนจริง ดังนั้น เซตของจำนวนเชิงซ้อนจึงเป็นฟีลด์ต่อเติม (field extension) ของเซตของจำนวนจริงโดยการเพิ่มรากของพหุนาม
ซึ่งไม่สามารถหาคำตอบได้ในเซตของจำนวนจริง ดังนั้น เซตของจำนวนเชิงซ้อนจึงเป็นฟีลด์ต่อเติม (field extension) ของเซตของจำนวนจริงโดยการเพิ่มรากของพหุนาม 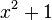 อีกนัยหนึ่ง เซตของจำนวนเชิงซ้อนคือริงผลหาร (quotient ring) ของริงพหุนาม
อีกนัยหนึ่ง เซตของจำนวนเชิงซ้อนคือริงผลหาร (quotient ring) ของริงพหุนาม ![\mathbb{R}[x]](http://upload.wikimedia.org/math/d/3/0/d30c4d8a82d45c0e3a53461a45ca72b5.png) กับไอดีล
กับไอดีล  เขียนเป็นประโยคสัญลักษณ์ได้ว่า
เขียนเป็นประโยคสัญลักษณ์ได้ว่า![\mathbb{C} = \mathbb{R}[x]/(x^2+1)](http://upload.wikimedia.org/math/5/a/c/5ac3abb6998c787c5115e49600c4e3b8.png)
ส่วนจริงและส่วนจินตภาพ
ถ้า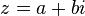 เราเรียก
เราเรียก  ว่า ส่วนจริง ของ
ว่า ส่วนจริง ของ  เขียนแทนด้วยสัญลักษณ์
เขียนแทนด้วยสัญลักษณ์  และเราเรียก
และเราเรียก  ว่า ส่วนจินตภาพ ของ
ว่า ส่วนจินตภาพ ของ  เขียนแทนด้วยสัญลักษณ์
เขียนแทนด้วยสัญลักษณ์  เราเรียกจำนวนเชิงซ้อนที่มีส่วนจริงเป็น 0 และส่วนจินตภาพไม่เป็น 0 ว่าจำนวนจินตภาพ (imaginary number)
เราเรียกจำนวนเชิงซ้อนที่มีส่วนจริงเป็น 0 และส่วนจินตภาพไม่เป็น 0 ว่าจำนวนจินตภาพ (imaginary number)สังยุคเชิงซ้อน[แก้]
ถ้า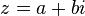 เป็นจำนวนเชิงซ้อน สังยุคของ
เป็นจำนวนเชิงซ้อน สังยุคของ  คือ
คือ  เราเขียนแทนสังยุคของ
เราเขียนแทนสังยุคของ  ด้วย
ด้วย 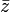 สังยุคของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้เมื่อ
สังยุคของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้เมื่อ ,
,  ,
, 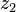 เป็นจำนวนเชิงซ้อนใดๆ
เป็นจำนวนเชิงซ้อนใดๆขนาดของจำนวนเชิงซ้อน
ขนาดของจำนวนเชิงซ้อน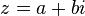 เขียนแทนด้วย
เขียนแทนด้วย 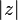 คือจำนวนจริงบวก
คือจำนวนจริงบวก  เราอาจแปลความหมายของขนาดของจำนวนเชิงซ้อนได้ว่าเป็นความยาวของเส้นตรงที่ลากจากจุด (0,0) ไปยังจุด (a,b) บนระนาบคาร์ทีเชียน ขนาดของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้
เราอาจแปลความหมายของขนาดของจำนวนเชิงซ้อนได้ว่าเป็นความยาวของเส้นตรงที่ลากจากจุด (0,0) ไปยังจุด (a,b) บนระนาบคาร์ทีเชียน ขนาดของจำนวนเชิงซ้อนมีสมบัติสำคัญๆ ดังต่อไปนี้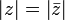


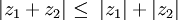 (อสมการสามเหลี่ยม)
(อสมการสามเหลี่ยม)
 ก็ต่อเมื่อ
ก็ต่อเมื่อ 
เมื่อ ,
,  , และ
, และ 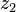 เป็นจำนวนเชิงซ้อนใดๆ จากสมบัติข้อที่สองและการแทนจำนวนจริง
เป็นจำนวนเชิงซ้อนใดๆ จากสมบัติข้อที่สองและการแทนจำนวนจริง  ด้วยจำนวนเชิงซ้อน
ด้วยจำนวนเชิงซ้อน  ทำให้เราได้ว่าถ้า
ทำให้เราได้ว่าถ้า 

ระนาบเชิงซ้อน
เรายังสามารถมองจำนวนเชิงซ้อนเป็นจุดหรือเวกเตอร์บนระนาบคาร์ทีเซียนสองมิติ และมักจะเรียกระนาบนี้ว่าระนาบเชิงซ้อน (complex plane) หรือผังของอาร์กานด์ ตามชื่อของ ชอง-โรแบร์ต อาร์กานด์ ผู้ค้นพบพิกัดคาร์ทีเซียนของจำนวนเชิงซ้อน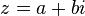 คือ
คือ  ในขณะที่พิกัดเชิงขั้วคิอ
ในขณะที่พิกัดเชิงขั้วคิอ 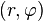 เมื่อ
เมื่อ  และ
และ  เป็นมุมที่เวกเตอร์
เป็นมุมที่เวกเตอร์  ทำกับแกน
ทำกับแกน  ในหน่วยเรเดียน เราเรียก
ในหน่วยเรเดียน เราเรียก  ว่า อาร์กิวเมนต์ของ
ว่า อาร์กิวเมนต์ของ  และเขียนแทนด้วยสัญลักษณ์
และเขียนแทนด้วยสัญลักษณ์  สังเกตว่าจำนวนเชิงซ้อนที่มีอาร์กิวเมนต์ต่างกันเท่ากับผลคูณของจำนวนเต็มกับ
สังเกตว่าจำนวนเชิงซ้อนที่มีอาร์กิวเมนต์ต่างกันเท่ากับผลคูณของจำนวนเต็มกับ  จะมีค่าเท่ากันสูตรของออยเลอร์ช่วยแสดงความสัมพันธ์ระหว่างพิกัดคาร์ทีเซียนและพิกัดเชิงขั้ว อีกทั้งยังช่วยให้เราสามารถเขียนจำนวนเชิงซ้อนได้อีกรูปแบบหนึ่งดังต่อไปนี้และเรายังสามารถพิสูจน์ได้ว่าและเมื่อ
จะมีค่าเท่ากันสูตรของออยเลอร์ช่วยแสดงความสัมพันธ์ระหว่างพิกัดคาร์ทีเซียนและพิกัดเชิงขั้ว อีกทั้งยังช่วยให้เราสามารถเขียนจำนวนเชิงซ้อนได้อีกรูปแบบหนึ่งดังต่อไปนี้และเรายังสามารถพิสูจน์ได้ว่าและเมื่อ ด้วยเหตุนี้เราจึงสามารถมองการคูณจำนวนเชิงซ้อนตัวหนึ่งๆ ว่าเป็นการหมุนและการยืด (หรือหด) เวกเตอร์ด้วยอาร์กิวเมนต์และขนาดของจำนวนเชิงซ้อนตัวนั้นตามลำดับการคูณด้วย
ด้วยเหตุนี้เราจึงสามารถมองการคูณจำนวนเชิงซ้อนตัวหนึ่งๆ ว่าเป็นการหมุนและการยืด (หรือหด) เวกเตอร์ด้วยอาร์กิวเมนต์และขนาดของจำนวนเชิงซ้อนตัวนั้นตามลำดับการคูณด้วย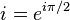 จึงสมมูลกับการหมุนเวกเตอร์ 90 องศาทวนเข็มนาฬิกา สมการ ฉะนั้นเราสามารถเข้าใจความหมายของสมการ
จึงสมมูลกับการหมุนเวกเตอร์ 90 องศาทวนเข็มนาฬิกา สมการ ฉะนั้นเราสามารถเข้าใจความหมายของสมการ  ได้อีกนัยหนึ่งว่า "การหมุน 90 องศาสองครั้งมีค่าเท่ากับการหมุน 180 องศา" หรือ "เมื่อหมุนเวกเตอร์
ได้อีกนัยหนึ่งว่า "การหมุน 90 องศาสองครั้งมีค่าเท่ากับการหมุน 180 องศา" หรือ "เมื่อหมุนเวกเตอร์  ไป 90 องศา ผลลัพธ์ที่ได้คือเวกเตอร์ (-1,0)"
ไป 90 องศา ผลลัพธ์ที่ได้คือเวกเตอร์ (-1,0)"การเรียงลำดับ
 ไม่เป็นฟีลด์อันดับ กล่าวคือเราไม่สามารถเรียงลำดับจำนวนเชิงซ้อนโดยที่การเรียงลำดับนั้นสอดคล้องกับการบวกและการคูณจำนวนเชิงซ้อนได้เลย
ไม่เป็นฟีลด์อันดับ กล่าวคือเราไม่สามารถเรียงลำดับจำนวนเชิงซ้อนโดยที่การเรียงลำดับนั้นสอดคล้องกับการบวกและการคูณจำนวนเชิงซ้อนได้เลยปริภูมิเวกเตอร์
อย่างที่ได้กล่าวไว้ข้างต้น เป็นปริภูมิเวกเตอร์สองมิติบน
เป็นปริภูมิเวกเตอร์สองมิติบน  เราได้ว่าการแปลงเชิงเส้นบน
เราได้ว่าการแปลงเชิงเส้นบน  (
( -linear map) ทุกตัวจะสามารถเขียนได้ในรูปเมื่อ
-linear map) ทุกตัวจะสามารถเขียนได้ในรูปเมื่อ และ
และ  เป็นจำนวนเชิงซ้อนใดๆ เราได้ว่าฟังก์ชัน
เป็นจำนวนเชิงซ้อนใดๆ เราได้ว่าฟังก์ชัน 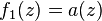 เป็นการหมุนและการยืดเวกเตอร์ ส่วนฟังก์ชัน
เป็นการหมุนและการยืดเวกเตอร์ ส่วนฟังก์ชัน 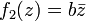 นั้นประกอบด้วยการหมุน การพลิก และการยืดเวกเตอร์ในฟังก์ชันเดียว สังเกตว่า
นั้นประกอบด้วยการหมุน การพลิก และการยืดเวกเตอร์ในฟังก์ชันเดียว สังเกตว่า 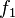 เท่านั้นที่เป็นการแปลงเชิงเส้นบน
เท่านั้นที่เป็นการแปลงเชิงเส้นบน  และเป็นฟังก์ชันโฮโลมอร์ฟิก เราสามารถหาอนุพันธ์ของ
และเป็นฟังก์ชันโฮโลมอร์ฟิก เราสามารถหาอนุพันธ์ของ 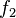 ได้ในเซตของจำนวนจริง แต่อนุพันธ์นั้นไม่สอดคล้องกับสมการโคชี-รีมันน์
ได้ในเซตของจำนวนจริง แต่อนุพันธ์นั้นไม่สอดคล้องกับสมการโคชี-รีมันน์สมบัติเชิงพีชคณิต
- มีแคแรกเทอริสติก 0
- มีดีกรีอดิศัยเมื่อเทียบกับฟีลด์เฉพาะใดๆ เท่ากับขนาดของเซตจำนวนจริง
- มีสมบัติการปิดเชิงพีชคณิต (ดู ทฤษฎีบทมูลฐานของพีชคณิต)
ด้วยเหตุนี้ จึงมีฟีลด์ย่อยแท้ที่สมสัณฐานกับตัวมันเองอยู่เป็นจำนวนมาก นอกจากนี้กาลอยด์กรุปของ
จึงมีฟีลด์ย่อยแท้ที่สมสัณฐานกับตัวมันเองอยู่เป็นจำนวนมาก นอกจากนี้กาลอยด์กรุปของ  บนเชตของจำนวนตรรกยะมีขนาดเท่ากับเซตกำลังของเซตของจำนวนจริง
บนเชตของจำนวนตรรกยะมีขนาดเท่ากับเซตกำลังของเซตของจำนวนจริง
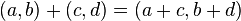
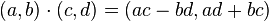
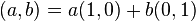








 ) จะมีลักษณะจำเพาะสามประการ ดังนี้
) จะมีลักษณะจำเพาะสามประการ ดังนี้
ไม่มีความคิดเห็น:
แสดงความคิดเห็น