ฟังก์ชันตรีโกณมิติ (อังกฤษ: Trigonometric function) คือ ฟังก์ชันของมุม ซึ่งมีความสำคัญในการศึกษารูปสามเหลี่ยมและปรากฏการณ์ในลักษณะเป็นคาบ ฟังก์ชันอาจนิยามด้วยอัตราส่วนของด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉาก หรืออัตราส่วนของพิกัดของจุดบนวงกลมหนึ่งหน่วย หรือนิยามในรูปทั่วไปเช่น อนุกรมอนันต์ หรือสมการเชิงอนุพันธ์ รูปสามเหลี่ยมที่นำมาใช้จะอยู่ในระนาบแบบยุคลิด ดังนั้น ผลรวมของมุมทุกมุมจึงเท่ากับ 180° เสมอ
ในปัจจุบัน มีฟังก์ชันตรีโกณมิติอยู่ 6 ฟังก์ชันที่นิยมใช้กันดังตารางข้างล่าง (สี่ฟังก์ชันสุดท้ายนิยามด้วยความสัมพันธ์กับฟังก์ชันอื่น แต่ก็สามารถนิยามด้วยเรขาคณิตได้)
| ฟังก์ชัน | ตัวย่อ | ความสัมพันธ์ |
| ไซน์ (Sine) | sin |  |
| โคไซน์ (Cosine) | cos |  |
| แทนเจนต์ (Tangent) | tan (หรือ tg) |  |
| โคแทนเจนต์ (Cotangent) | cot (หรือ ctg หรือ ctn) |  |
| ซีแคนต์ (Secant) | sec |  |
| โคซีแคนต์ (Cosecant) | csc (หรือ cosec) |  |
ความสัมพันธ์ระหว่างฟังก์ชันเหล่านี้ อยู่ในบทความเรื่อง เอกลักษณ์ตรีโกณมิติ
นิยามจากรูปสามเหลี่ยมมุมฉาก
ในการนิยามฟังก์ชันตรีโกณมิติสำหรับมุม A เราจะกำหนดให้มุมใดมุมหนึ่งในรูปสามเหลี่ยมมุมฉากเป็นมุม A
เรียกชื่อด้านแต่ละด้านของรูปสามเหลี่ยมตามนี้
- ด้านตรงข้ามมุมฉาก (hypotenuse) คือด้านที่อยู่ตรงข้ามมุมฉาก หรือเป็นด้านที่ยาวที่สุดของรูปสามเหลี่ยมมุมฉาก ในที่นี้คือ h
- ด้านตรงข้าม (opposite side) คือด้านที่อยู่ตรงข้ามมุมที่เราสนใจ ในที่นี้คือ a
- ด้านประชิด (adjacent side) คือด้านที่อยู่ติดกับมุมที่เราสนใจและมุมฉาก ในที่นี้คือ b
จะได้
1). ไซน์ ของมุม คือ อัตราส่วนของความยาวด้านตรงข้าม ต่อความยาวด้านตรงข้ามมุมฉาก ในที่นี้คือ
- sin(A) = ข้าม/ฉาก = a/h
2). โคไซน์ ของมุม คือ อัตราส่วนของความยาวด้านประชิด ต่อความยาวด้านตรงข้ามมุมฉาก ในที่นี้คือ
- cos(A) = ชิด/ฉาก = b/h
3). แทนเจนต์ ของมุม คือ อัตราส่วนของความยาวด้านตรงข้าม ต่อความยาวด้านประชิด ในที่นี้คือ
- tan(A) = ข้าม/ชิด = a/b
4). โคซีแคนต์ csc(A) คือฟังก์ชันผกผันการคูณของ sin(A) นั่นคือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านตรงข้าม
- csc(A) = ฉาก/ข้าม = h/a
5). ซีแคนต์ sec(A) คือฟังก์ชันผกผันการคูณของ cos(A) นั่นคือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านประชิด
- sec(A) = ฉาก/ชิด = h/b
6). โคแทนเจนต์ cot(A) คือฟังก์ชันผกผันการคูณของ tan(A) นั่นคือ อัตราส่วนของความยาวด้านประชิด ต่อความยาวด้านตรงข้าม
- cot(A) = ชิด/ข้าม = b/a
วิธีจำ
วิธีจำอย่างง่าย ๆ คือจำว่า ข้ามฉาก ชิดฉาก ข้ามชิด ซึ่งหมายความว่า
- ข้ามฉาก ... sin = ด้านตรงข้าม/ด้านตรงข้ามมุมฉาก
- ชิดฉาก ... cos = ด้านประชิด/ด้านตรงข้ามมุมฉาก
- ข้ามชิด ... tan = ด้านตรงข้าม/ด้านประชิด
นิยามด้วยวงกลมหนึ่งหน่วย
ฟังก์ชันตรีโกณมิติทั้ง 6 ฟังก์ชัน สามารถนิยามด้วยวงกลมหนึ่งหน่วย ซึ่งเป็นวงกลมที่มีรัศมียาว 1 หน่วย และมีจุดศูนย์กลางอยู่ที่จุดกำเนิด วงกลมหนึ่งหน่วยช่วยในการคำนวณ และหาค่าฟังก์ชันตรีโกณมิติสำหรับอาร์กิวเมนต์ที่เป็นบวกและลบได้ ไม่ใช่แค่ 0 ถึง π/2 เรเดียนเท่านั้น สมการของวงกลมหนึ่งหน่วยคือ:จากรูป เราจะวัดมุมในหน่วยเรเดียน โดยให้มุมเป็นบวกในทิศทวนเข็มนาฬิกา และมุมเป็นลบในทิศตามเข็มนาฬิกา ลากเส้นให้ทำมุม θ กับแกน x ด้านบวก และตัดกับวงกลมหนึ่งหน่วย จะได้ว่าพิกัด x และ y ของจุดตัดนี้จะเท่ากับ cos θ และ sin θ ตามลำดับ เหตุผลเพราะว่ารูปสามเหลี่ยมที่เกิดขึ้นนั้น จะมีความยาวด้านตรงข้ามมุมฉาก ยาวเท่ากับรัศมีวงกลม นั่นคือยาวเท่ากับ 1 หน่วย เราจะได้ sin θ = y/1 และ cos θ = x/1 วงกลมหนึ่งหน่วยช่วยให้เราหากรณีที่สามเหลี่ยมมีความสูงเป็นอนันต์ (เช่น มุม π/2 เรเดียน) โดยการเปลี่ยนความยาวของด้านประกอบมุมฉาก แต่ด้านตรงข้ามมุมฉากยังยาวเท่ากับ 1 หน่วย เท่าเดิมสำหรับมุมที่มากกว่า 2π หรือต่ำกว่า −2π เราสามารถวัดมุมได้ในวงกลม ด้วยวิธีนี้ ค่าไซน์และโคไซน์จึงเป็นฟังก์ชันเป็นคาบที่มีคาบเท่ากับ 2π:เมื่อ θ เป็นมุมใดๆ และ k เป็นจำนวนเต็มใดๆคาบที่เป็นบวกที่เล็กที่สุดของฟังก์ชันเป็นคาบ เรียกว่า คาบปฐมฐานของฟังก์ชัน คาบปฐมฐานของไซน์, โคไซน์, ซีแคนต์ หรือโคซีแคนต์ จะเท่ากับวงกลมหนึ่งวง นั่นคือเท่ากับ 2π เรเดียน หรือ 360 องศา คาบปฐมฐานของแทนเจนต์ หรือโคแทนเจนต์ จะเท่ากับครึ่งวงกลม นั่นคือเท่ากับ π เรเดียน หรือ 180 องศาจากข้างบนนี้ ค่าไซน์และโคไซน์ถูกนิยามจากวงกลมหนึ่งหน่วยโดยตรง แต่สี่ฟังก์ชันตรีโกณมิติที่เหลือจะถูกนิยามโดยฟังก์ชันตรีโกณมิติพื้นฐานทั้งหมด สามารถนิยามจากวงกลมหนึ่งหน่วยได้โดยใช้วงกลมหนึ่งหน่วย ที่จุดศูนย์กลางอยู่ที่จุด O (ตามรูปทางขวา) ซึ่งคล้ายกับการนิยามเชิงเรขาคณิตที่ใช้กันมาในสมัยก่อน ให้ AB เป็นคอร์ดของวงกลม ซึ่ง θ เป็นครึ่งหนึ่งของมุมที่รองรับคอร์ดนั้น จะได้- sin(θ) คือ ความยาว AC (ครึ่งหนึ่งของคอร์ด) นิยามนี้เริ่มใช้โดยชาวอินเดีย
- cos(θ) คือระยะทางตามแนวนอน OC
- versin(θ) = 1 − cos(θ) คือ ความยาว CD
- tan(θ) คือ ความยาวของส่วน AE ของเส้นสัมผัสที่ลากผ่านจุด A จึงเป็นที่มาของคำว่าแทนเจนต์นั่นเอง (tangent = สัมผัส)
- cot(θ) คือ ส่วนของเส้นสัมผัสที่เหลือ คือความยาว AF
- sec(θ) = OE และ
- csc(θ) = OF เป็นส่วนของเส้นซีแคนต์ (ตัดวงกลมที่จุดสองจุด) ซึ่งสามารถมองว่าเป็นภาพฉายของ OA ตามแนวเส้นสัมผัสที่จุด A ไปยังแกนนอนและแกนตั้ง ตามลำดับ
- exsec(θ) = DE = sec(θ) − 1 (ส่วนของซีแคนต์ด้านนอก)
ด้วยวิธีสร้างเหล่านี้ ทำให้เห็นภาพฟังก์ชันซีแคนต์และแทนเจนต์ลู่ออก เมื่อ θ เข้าใกล้ π/2 (90 องศา) และโคซีแคนต์และโคแทนเจนต์ลู่ออก เมื่อ θ เข้าใกล้ศูนย์ (เราสามารถพิสูจน์เอกลักษณ์ตรีโกณมิติด้วยรูปภาพได้)นิยามด้วยอนุกรม
โดยการใช้เรขาคณิตและคุณสมบัติของลิมิต เราแสดงได้ว่าอนุพันธ์ของไซน์คือโคไซน์ และอนุพันธ์ของไคโซน์คือค่าลบชองไซน์ เราสามารถใช้อนุกรมเทย์เลอร์สำหรับแสดงเอกลักษณ์ต่อไปนี้สำหรับทุกจำนวนจริง x:เอกลักษณ์เหล่านี้มักใช้เป็น นิยาม ของฟังก์ชันไซน์ และโคไซน์ ซึ่งนำไปใช้เป็นจุดเริ่มต้นแบบเข้มของฟังก์ชันตรีโกณมิติ และการประยุกต์ของมัน (เช่น อนุกรมฟูรีเย) เพราะว่ามันมีพื้นฐานอยู่บนระบบจำนวนจริง ไม่ขึ้นกับการตีความทางเรขาคณิตใดๆ การหาอนุพันธ์ได้และความต่อเนื่องของฟังก์ชันก็มาจากนิยามนี้เอกลักษณ์





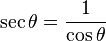
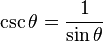
















ไม่มีความคิดเห็น:
แสดงความคิดเห็น